Skip to contents

debkeepr

CRAN status R-CMD-check Coverage status Lifecycle: stable

debkeepr integrates non-decimal currencies that use tripartite and tetrapartite systems into the methodologies of Digital Humanities and the practices of reproducible research. The package makes it possible for historical non-decimal currencies, such as the tripartite system of pounds, shillings, and pence, to behave like decimalized numeric values through the implementation of the deb_lsd, deb_tetra, and deb_decimal vector types. These types are based on the infrastructure provided by the vctrs package. debkkeepr simplifies the process of performing arithmetic calculations with non-decimal currencies — such as adding £3 13s. 4d. sterling to £8 15s. 9d. sterling — and also provides a basis for analyzing account books with thousands of transactions recorded in non-decimal currencies. The name of the debkeepr package derives from this latter capability of analyzing historical account books that often used double-entry bookkeeping.

Installation

Install the released version of debkeepr from CRAN:

install.packages("debkeepr")

Or install the development version from GitHub with:

# install.packages("pak")
pak::pak("jessesadler/debkeepr")

Please open an issue if you have any questions, comments, or requests.

Historical Background

The debkeepr package uses the nomenclature of l, s, and d to represent pounds, shillings, and pence units in non-decimal currencies. The abbreviations derive from the Latin terms libra, solidus, and denarius. The libra was a Roman measurement of weight, while the solidus and denarius were both Roman coins. The denarius was a silver coin from the era of the Republic, in contrast to the golden solidus that was issued in the Late Empire. As the production of silver coins overtook that of gold by the 8th century, a solidus came to represent 12 silver denarii coins, and 240 denarii were — for a time — made from one libra or pound of silver. The custom of counting coins in dozens (solidi) and scores of dozens (librae) spread throughout the Carolingian Empire and became ingrained in much of Europe. However, a variety of currencies or monies of account used other bases for the solidus and denarius units. Some currencies and other value systems, such as those for weights, added a fourth unit. debkeepr provides a consistent manner for dealing with any set of bases within tripartite or tetrapartite systems through the bases attribute of deb_lsd, deb_tetra, and deb_decimal vectors.

Translations of libra, solidus, and denarius units:

  • English: pounds, shillings, pence
  • French: livres, sols or sous, deniers
  • Italian: lire, soldi, denari
  • Flemish: ponden, schellingen, groten
  • Dutch: guilders, stuivers, penningen

Resources

Usage

The deb_lsd, deb_tetra, and deb_decimal types are implemented to deal with two interrelated problems inherent in historical non-decimal currencies and other value systems.

  1. Historical currencies consist of three or four separate non-decimal units. Most often: pounds, shillings, and pence with sometimes a fourth unit, such as the farthing, added on.
  2. The bases of the shillings, pence, and optionally farthing units differed by region, coinage, and era.

The deb_lsd type maintains the tripartite structure of non-decimal currencies and provides a bases attribute to record the bases for the shillings and pence units. The deb_tetra type extends the concept of the deb_lsd type to incorporate currencies and other types of values that consist of four units. The deb_decimal type provides a means to decimalize both deb_lsd and deb_tetra types while keeping track of the two or three non-decimal bases and the unit represented as attributes.

Let’s see how this works in practice, beginning with deb_lsd vectors. Note that all of the functions in debkeepr begin with the prefix deb_, which is short for double-entry bookkeeping.

library(debkeepr)

# Create deb_lsd vectors with standard bases of 20s. 12d.
lsd1 <- deb_lsd(l = 3, s = 13, d = 4)
lsd2 <- deb_lsd(l = 8, s = 15, d = 9)

# Combine multiple values together
c(lsd1, lsd2)
#> <deb_lsd[2]>
#> [1] 3:13s:4d 8:15s:9d
#> # Bases: 20s 12d

deb_tetra vectors work similarly but add an f unit that defaults to a base of four.

# Create deb_tetra vectors with standard bases of 20s. 12d. 4f.
tetra1 <- deb_tetra(l = 3, s = 13, d = 4, f = 3)
tetra2 <- deb_tetra(l = 8, s = 15, d = 9, f = 2)

A primary reason for the creation of the deb_lsd and deb_tetra types is to simplify arithmetic calculations with non-decimal currency. Doing calculations by hand requires the use of compound unit arithmetic and normalization.

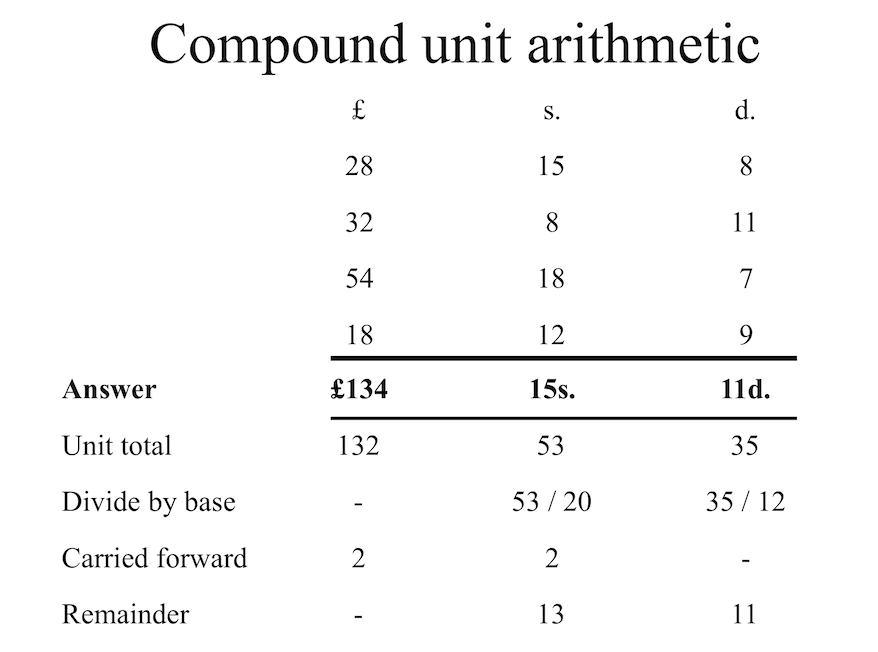
All implemented arithmetic calculations with deb_lsd and deb_tetra types — sum(), round(), +, -, etc. — automatically normalize the values according to the bases attribute. In addition, you can manually normalize non-standard values with deb_normalize().

# Perform arithmetic
lsd1 + lsd2
#> <deb_lsd[1]>
#> [1] 12:9s:1d
#> # Bases: 20s 12d
lsd2 - lsd1
#> <deb_lsd[1]>
#> [1] 5:2s:5d
#> # Bases: 20s 12d
lsd2 * 2 - lsd1
#> <deb_lsd[1]>
#> [1] 13:18s:2d
#> # Bases: 20s 12d
tetra2 + tetra1
#> <deb_tetra[1]>
#> [1] 12:9s:2d:1f
#> # Bases: 20s 12d 4f

# Normalize a non-standard value to default bases
deb_normalize(deb_lsd(132, 53, 35))
#> <deb_lsd[1]>
#> [1] 134:15s:11d
#> # Bases: 20s 12d

# Can also normalize numeric vectors of length 3 or 4
# Must provide the bases for tetrapartite value
deb_normalize(c(132, 53, 35, 18), bases = c(20, 12, 4))
#> <deb_tetra[1]>
#> [1] 134:16s:3d:2f
#> # Bases: 20s 12d 4f

All types allow the user to define the bases for the solidus, denarius, and optionally farthing units of values, enabling integration of currencies that do not use the standardized bases. For example, the Polish florin found in Dafforne’s practice journal used the non-standard bases of 30 gros of 18 denars.

# Create deb_lsd vector with standard bases of 20s. 12d.
(lsd3 <- deb_lsd(l = c(28, 32, 54, 18),
                 s = c(15, 8, 18, 12),
                 d = c(8, 11, 7, 9)))
#> <deb_lsd[4]>
#> [1] 28:15s:8d 32:8s:11d 54:18s:7d 18:12s:9d
#> # Bases: 20s 12d

# Same numerical values as Polish florins
(florins <- deb_lsd(l = c(28, 32, 54, 18),
                    s = c(15, 8, 18, 12),
                    d = c(8, 11, 7, 9),
                    bases = c(30, 18)))
#> <deb_lsd[4]>
#> [1] 28:15s:8d 32:8s:11d 54:18s:7d 18:12s:9d
#> # Bases: 30s 18d

# Different outcome with sum due to the different bases
sum(lsd3)
#> <deb_lsd[1]>
#> [1] 134:15s:11d
#> # Bases: 20s 12d
sum(florins)
#> <deb_lsd[1]>
#> [1] 133:24s:17d
#> # Bases: 30s 18d

# Vectors with different bases cannot be combined since
# their relationship is unknown. Doing so results in an error.
sum(lsd3, florins)
#> Error:
#> ! Incompatible `bases`.
#> ℹ `bases` must be compatible to combine <deb_lsd>, <deb_tetra>, or
#>   <deb_decimal> vectors.
#> ✖ Cannot combine: `..1` <deb_lsd> vector with `bases` s = 20 and d = 12.
#> ✖ Cannot combine: `..2` <deb_lsd> vector with `bases` s = 30 and d = 18.
#> ℹ Use `deb_convert_bases()` to convert one or more of the vectors to compatible
#>   `bases`.

deb_decimal vectors represent non-decimal values in the more familiar decimal form. Internally, deb_decimal vectors are built on double() vectors. These decimalized vectors are linked to their non-decimal form through the unit and bases attributes. They can represent either tripartite or tetrapartite values. The only differences are the length of the bases (2 or 3) and the option to choose the “f” unit with tetrapartite values.

# Create deb_decimal from numeric vector
(dec1 <- deb_decimal(c(5.525, 12.235, 8.45)))
#> <deb_decimal[3]>
#> [1]  5.525 12.235  8.450
#> # Unit: libra
#> # Bases: 20s 12d

# Same currency values in solidus unit
(dec2 <- deb_decimal(c(110.5, 244.7, 169), unit = "s"))
#> <deb_decimal[3]>
#> [1] 110.5 244.7 169.0
#> # Unit: solidus
#> # Bases: 20s 12d

# Equality between different units
dec1 == dec2
#> [1] TRUE TRUE TRUE

# Use the bases argument to create tetrapartite values
deb_decimal(c(5.525, 12.235, 8.45), bases = c(20, 12, 4))
#> <deb_decimal[3]>
#> [1]  5.525 12.235  8.450
#> # Unit: libra
#> # Bases: 20s 12d 4f

# Equality between deb_lsd and deb_decimal vectors
# £5 10s. 6d. is equal to 1,326 pence
deb_lsd(5, 10, 6) == deb_decimal(1326, unit = "d")
#> [1] TRUE

# Which is also equal to 5,304 farthings with default tetrapartite bases
deb_lsd(5, 10, 6) == deb_decimal(5304, unit = "f", bases = c(20, 12, 4))
#> [1] TRUE

When working with decimalized data is preferable, the deb_decimal type makes casting from and to deb_lsd or deb_tetra possible without losing any metadata about the bases and therefore the actual value being represented. deb_lsd, deb_tetra, and deb_decimal vectors can also be combined with numeric vectors or cast from and to numeric vectors. debkeepr uses an internal conversion hierarchy of numeric() -> deb_decimal() -> deb_tetra -> deb_lsd().

# deb_decimal -> deb_lsd
c(dec1, lsd1, lsd2)
#> <deb_lsd[5]>
#> [1] 5:10s:6d   12:4s:8.4d 8:9s:0d    3:13s:4d   8:15s:9d  
#> # Bases: 20s 12d
# deb_decimal -> deb_tetra
c(dec1, tetra1, 8.25)
#> <deb_tetra[5]>
#> [1] 5:10s:6d:0f   12:4s:8d:1.6f 8:9s:0d:0f    3:13s:4d:3f   8:5s:0d:0f   
#> # Bases: 20s 12d 4f
# deb_decimal -> deb_tetra -> deb_lsd
c(dec1, tetra1, lsd2)
#> <deb_lsd[5]>
#> [1] 5:10s:6d    12:4s:8.4d  8:9s:0d     3:13s:4.75d 8:15s:9d   
#> # Bases: 20s 12d

# Cast between deb_lsd, deb_tetra, and deb_decimal vectors
deb_as_lsd(dec1)
#> <deb_lsd[3]>
#> [1] 5:10s:6d   12:4s:8.4d 8:9s:0d   
#> # Bases: 20s 12d
deb_as_decimal(florins)
#> <deb_decimal[4]>
#> [1] 28.51481 32.28704 54.61296 18.41667
#> # Unit: libra
#> # Bases: 30s 18d
deb_as_decimal(tetra2)
#> <deb_decimal[1]>
#> [1] 8.789583
#> # Unit: libra
#> # Bases: 20s 12d 4f
# Provide an f unit base to cast from tripartite to tetrapartite
deb_as_tetra(lsd1, f = 4)
#> <deb_tetra[1]>
#> [1] 3:13s:4d:0f
#> # Bases: 20s 12d 4f

# Represented by solidus/shillings unit
deb_as_decimal(lsd3, unit = "s")
#> <deb_decimal[4]>
#> [1]  575.6667  648.9167 1098.5833  372.7500
#> # Unit: solidus
#> # Bases: 20s 12d

# Only tetrapartite values can be represented by the farthings unit
deb_as_decimal(tetra1, unit = "f")
#> <deb_decimal[1]>
#> [1] 3523
#> # Unit: farthing
#> # Bases: 20s 12d 4f

# All three types can be cast to base numeric, which,
# of course, leads to the loss of all metadata
as.numeric(lsd3)
#> [1] 28.78333 32.44583 54.92917 18.63750
as.numeric(tetra1)
#> [1] 3.669792
as.numeric(dec1)
#> [1]  5.525 12.235  8.450

Comparing deb_lsd, deb_tetra, and deb_decimal vectors

See the Getting Started with debkeepr vignette for an in depth discussion of the similarities and differences between the two types.

  • The deb_lsd and deb_tetra types have the advantage of maintaining the structure and values used by non-decimal currencies, making it easier to identify and present such values.
  • deb_decimal implements a wider array of mathematical functions and arithmetic operations than deb_lsd or deb_tetra.
  • You can move between deb_lsd or deb_tetra types and the deb_decimal type without losing any data through deb_as_lsd(), deb_as_tetra(), and deb_as_decimal() casting methods.
  • Because deb_lsd, deb_tetra, and deb_decimal are based on the vctrs package, all types act as expected in data frames or tibbles columns. From dplyr 1.0.0 — which is the minimal version used by debkeepr — all dplyr functions work on both debkeepr types.
  • ggplot2 does not know how to pick a scale for deb_lsd or deb_tetra types. In contrast, deb_decimal vectors work properly with ggplot2, though explicitly identifying the scale as continuous — with scale_y_continuous() or scale_x_continuous() — is needed to avoid the appearance of a message.
  • deb_lsd, deb_tetra, and deb_decimal vectors cannot be combined in a single function if their bases differ. Tripartite and tetrapartite values can be combined if the bases of their solidus and denarius bases match. The only way to transform the bases of deb_lsd, deb_tetra, and deb_decimal vectors is explicitly with deb_convert_bases(). This prevents mistakenly combining two different currencies together without properly converting their values.